I-V曲線校正方法-基于SDM的數(shù)值方法：

校正程序 

表1總結(jié)了所有被研究和實現(xiàn)的方法，并將其分為前8個類（A、B、C、D、E、F、G或H）之 一。對于每種方法，還包括了所需的內(nèi)在系數(shù)的列表。為了澄清這些系數(shù)的含義，表2包含了每 個所需的內(nèi)在系數(shù)的一行，并提供了一種如果制造商沒有提供的方法來估計其值的參考。在本 節(jié)的其余部分，將簡要解釋每一種研究的方法，提供要應用的方程。

C01：理想單二極管模型 

與任何數(shù)值方法一樣，這種方法都是基于太陽能電池的物理模型。模擬光伏器件I-V特性 曲線的Z擴展的底層模型是單二極管模型（SDM），它包括一個電流源、一個二極管和兩個寄生 電阻：串聯(lián)電阻Rs和并聯(lián)或并聯(lián)電阻Rsh（見圖1）。然而，可以在文獻中找到一些簡化的方法 ，其中一種或兩種寄生電阻都被忽略了。在D一種方法中，將解決SDM的Z簡單版本，稱為“三 參數(shù)模型”（我們稱為理想的SDM或ISDM），而不包括任何寄生抗性，i。e., 假設串聯(lián)電阻為 接收站= 0 W和平行電阻可以去除(Rsh! ￥).與該模型相關的數(shù)學表達式（式（75）：

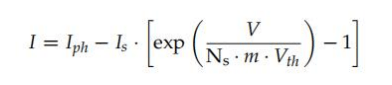
可以看出，從實驗曲線的I-V對中只能確定三個未知參數(shù)：光生成電流Iph、暗飽和電流Is 和二極管理想因子m。Z初，這些參數(shù)的值是指初始條件(G1，T1)可以估計。但是，將這些參數(shù) 的值校正到固定的參考條件可能非常方便，例如STC。事實上，有一些表達式用于將這些參數(shù)從 測量條件（G，T）轉(zhuǎn)換為(GSTC, TSTC)，反之亦然。許多作者[49,87,88]提供了相當于（方程 （76））的表達式來糾正Iph，而可以找到不同的方法來表示的依賴性是對器件溫度T，類似于 （式（77）)。

其中q = 1.602176634 10 19在這種情況下，應該假定為一個從eV轉(zhuǎn)換為焦耳的無量綱因子 。 使用（公式（76）-（79）），可以將這些參數(shù)轉(zhuǎn)換為任何參數(shù)(G2、T2)，這樣模型就可 以模擬任何期望目標條件下的I-V曲線。因此，目標是利用(G1，T1)，以便稍后模擬在(G2，T2). 從一個離散的I-V對集合中識別參數(shù)可以使用一個數(shù)值曲線擬合程序來執(zhí)行（例如，包括在 Matlab[19]的優(yōu)化工具箱中）。

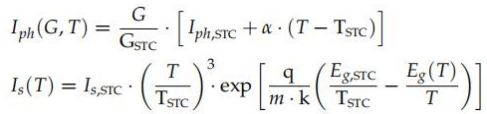
C02：簡化的單二極管模型 

在文獻中，有報道稱后者的ISDM可能非常不準確，因此許多作者提出了包括一系列電阻Rs ，而只忽略了平行電阻Rsh，如圖3所示。該模型的行為使用（公式（78）)進行描述：

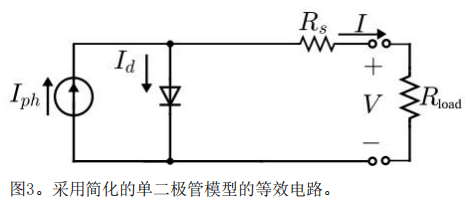
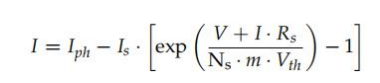
因此，有四個未知參數(shù)：(Iph,是, m, Rs).Z后，這些數(shù)值方法大多都假設了級數(shù)電阻 接收站作為一個常數(shù)的內(nèi)在參數(shù)（式（79）)，不依賴于G或T。

接收站=接收站,STC

C03：單二極管模型 

復雜性的下一步可以通過假設存在一個并行電阻Rsh來實現(xiàn)，從而得到一個與圖1中所示的 等效電路，它對應于其“五參數(shù)”版本中的經(jīng)典單二極管模型（方程(9)）。在這種情況下，使 用擬合工具的方程組由（公式(9)、（76）、（77）、（79）和（80）)組成，假設平行電阻Rsh 也是恒定的：Rsh=Rsh,STC

C04：單二極管型號(b) 

該方法試圖對前一種方法進行改進。雖然串聯(lián)電阻接收站繼續(xù)被認為是一個常數(shù)，對于平 行電阻Rsh，對輻照度G的依賴通過（式（81）)表示：

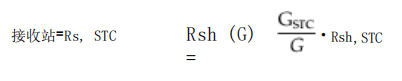
C05：拉斯切爾方程 

基于實驗數(shù)據(jù)，Ruschel等人。[18]指出，由于低輻照度水平的非線性行為，以前的方法 對于平行電阻不夠準確。因此，在那篇論文中，有一個替代的翻譯方程Rsh提出，引入兩個額 外的擬合參數(shù)，h和λ，它們依賴于單元技術（式（82））：

C06： PVSYST方法 

PVsyst是一個軟件，它實現(xiàn)了多個模型，供工程師用于設計不同類型的光伏項目[89]。為 了解決與平行電阻Rsh建模所產(chǎn)生的困難有關的問題，在本軟件[52]中使用了表達式（等式（8 3））：

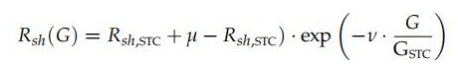
其中，m和ν是每種不同技術必須事先知道的值，以及Rsh, STC（平行電阻Rsh在GSTC= 1000 W/m 2)應在從初始曲線中識別其他參數(shù)時確定。 后一個公式可以簡化，假設m和m之間的固定比率RRsh,STC，以這種方式，（式（83）)可 以重寫為（式（84））[18]（每種技術應給出此比率R，而不是m）：

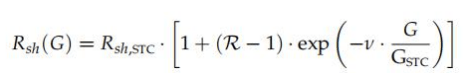
C07：沃克方程 

雖然這是Z廣為人知的方程來表示暗飽和電流之間的關系是而器件溫度T為（式（77）） ，其他作者[53,90]更傾向于使用一個稍微不同的表達式，其中T的比值/TSTC提高3/m（而不是 僅提高3），因為這種替代方法似乎更適合相同情況下的實驗數(shù)據(jù)（式（85）)：

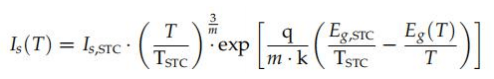
因此，本文提到的作為C07的方法正是使用（公式(9)、（76）、（79）、（84）和（85）) 在STC條件下確定五個未知參數(shù)進行曲線擬合的結(jié)果。 

C08：勞里諾方法 

為了提高精度，一些作者還包括了串聯(lián)電阻的額外依賴性接收站設備溫度。這就是勞里諾 等人的情況。[54]，其中通過串聯(lián)電阻Rs的溫度系數(shù)k假設有直接的線性依賴，僅在他們自己的 IEC 60891：2021 [3]中引入（程序1和2）。事實上，（式（57）)也被建議使用（式（76）)、 （式（84）和（85）)來轉(zhuǎn)換固有系數(shù)。 

C09：丁的表達 

經(jīng)過深入的分析后，Ding等人。[55]給出了一個模擬串聯(lián)電阻的表達式接收站作為溫度的 函數(shù)（式（86）)：

Rs (T) = Rs0K· exp (Bs · T)

其中假設T用開爾文表示，接收站0K是在0k時的串聯(lián)電阻，和生于是一個必須從實驗數(shù)據(jù)中擬合的參數(shù)。在這種方法中，而不是確定的值接收站,STC，其目的是進行估計接收站0K. 

C10：Cotfas方法 

該方法使用（公式（76）、（77）和（80）)進行翻譯Iph，Is和Rsh，而它提出了系列抗 性Rs的替代表達式，它不僅依賴于T，也依賴于G（式（87））：

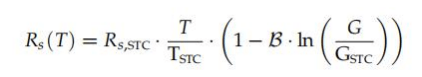
其中假設T用kelvin表示，B=為0.271（在原論文中稱為β）假設為常數(shù)。 Z后，方法C11、C12、C13、C14、C15分別與方法C01、C02、C06、C07、C08完全相同，僅改變（式（88））（式（88））， 這也是基于方法A10：

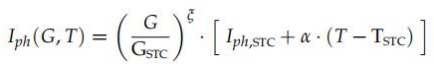
其中x，如前面所述，只是一個擬合參數(shù)，它解釋了光誘導電流Iph和輻照度G之間可能的非線性。x的值應該由實驗數(shù)據(jù)來確定，因為它不是由制造商提供的。

鏈接：IEC60891和其他溫度和輻照度校正程序與光伏器件I-V特性的比較